How is LLaMa.cpp possible?
Note: Substack doesn’t have great support for LaTeX, so you might want to read this article on my blog instead.
Recently, a project rewrote the LLaMa inference code in raw C++. With some optimizations and by quantizing the weights, the project allows running LLaMa locally on a wild variety of hardware:
On a Pixel5, you can run the 7B parameter model at 1 tokens/s.
On a M2 Macbook Pro, you can get ~16 tokens/s with the 7B parameter model
You can even run the 7B model on a 4GB RAM Raspberry Pi, albeit at 0.1 tokens/s.
If you are like me, you saw this and thought: What? How is this possible? Don’t large models require expensive GPUs? I took my confusion and dove into the math surrounding inference requirements to understand the constraints we’re dealing with.
Let’s start with GPUs. GPUs have two main benefits for deep learning:
They have a large amount of memory bandwidth (A100: 1935 GB/s, 4090: 1008 GB/s)
They have a large amount of compute (A100: 312 TFLOPS of FP16, 4090: 82.6 TFLOPS of FP16)
When we talk about memory bandwidth, we’re talking about how long it takes to move things from the HBM memory (i.e. the RAM) into the on-chip memory. To actually do math with the GPU, we need to move the matrices in question into the on-chip memory, which is quite small (40MB on an A100, compared to 40-80GB of RAM). The memory bandwidth is ~2 orders of magnitude smaller than the compute performance— this will matter later, as the memory bandwidth tends to be the bottleneck for inference.
What does this mean in the context of serving LLaMa? Let’s start with some inference arithmetic. We can do some rough calculations on the inference performance of a LLM using Kipply’s article.1 First, some notation on the dimensions of the model:
The Q, K, and V weight matrices are all shape [ d_model, d_head], and we have n_heads of them per layer; the attention output matrix has the same shape, for a total of 4 * [ d_model, n_heads * d_head]. By convention, GPT-style networks have d_head * n_heads = d_model.
The MLP has two weight matrices, of shape [model_dim, 4 * model_dim] and
[4 * model_dim, model]
The embedding matrix is of size [vocab, model_dim].
This gives us a handy equation for the number of parameters in a GPT-style model:2
For the duration of the post, I’m going to focus on the case where we’re running a ChatGPT style service locally, which is what LLaMa.cpp does, letting me assume a batch size of 1.
For efficient inference, the KV cache has to be stored in memory; the KV cache requires storing the KV values for every layer, which is equal to storing:
I use n_bytes here to indicate the number of bytes per param; for float32s, this is 4, for float16s, this is 2, etc. The 2 in the middle is because we have to store one set of weights for the K values, and one for the Vs.
Given a model with n layers, the total memory for the KV cache is:
In addition to storing the KV cache in memory, we also need to store the weights themselves in memory; this requires n_bytes * P bytes.
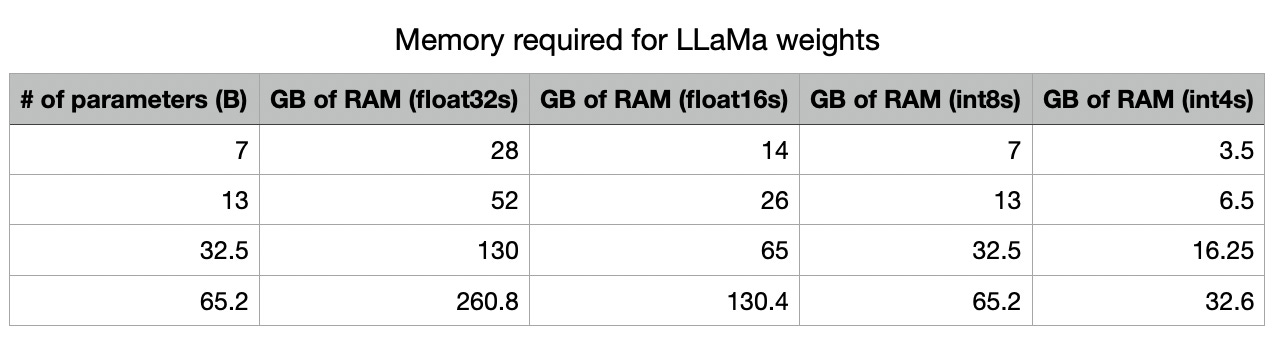
This is one of the key advantages of quantization. By using less precision, we can radically decrease the amount of memory needed to store our models in memory. Note that, with int4 precision, all of these models fit into memory on an A100 (which is the standard datacenter GPU right now), and all of them, except for the biggest model, fit into memory on high-end consumer GPUs (3090s/4090s, which have 24GB of RAM).
Now, when it comes to actually running inferece, it takes approximately 2P FLOPS per token, because we are doing a bunch of matmuls with a total of P parameters, and multiplying a matrix of size (m, n) with a vector of size (n,) has a cost of 2mn.3
With all that math out of the way, let’s calculate the requirements for running inference with LLaMa. The main requirements when it comes to sampling are:
Keep the KV cache in memory, in addition to all the parameters.
Read all the weights from HBM into the on-chip memory. Because we sample auto-regressively, we have to repeat this for each token we sample.
Do the actual matmuls to calculate the output of our network.
The latency is the maximum of either the compute or the memory latency, as reading parameters into on-chip memory happens asynchronously in all modern tensor programming libraries. As a result, we write:
where B is the batch size. As the memory bandwidth is ~1.935e12, and the number of FLOPS is ~3.12e14, as long as the batch size is less than 161, the model is memory-bound.
With a batch size of 1, this is the same equation, as on most hardware (e.g. Nvidia GPUs), there is a linear speedup as you decrease the precision (you get twice the FLOPS when using fp16 vs fp32, which doubles again as you go to int8, and doubles once more as you go to int4s).
As LLaMa.cpp uses int4s, the RAM requirements are reduced to 1.33GB of memory for the KV cache, and 16.25GB of VRAM for the model parameters. That’s pretty good!
As the memory bandwidth is almost always4 much smaller than the number of FLOPS, memory bandwidth is the binding constraint.
Note that the number of FLOPS/token is identical to the memory bandwidth required, as we have to 1) load all of the parameters into on-chip memory and then 2) use the parameters to compute the results. These happen simultaneously, as all modern tensor programming frameworks are able to handle the “loading into memory” bit asynchronously, so the total time required is max(compute time, memory time).
Running LLaMa on an A100
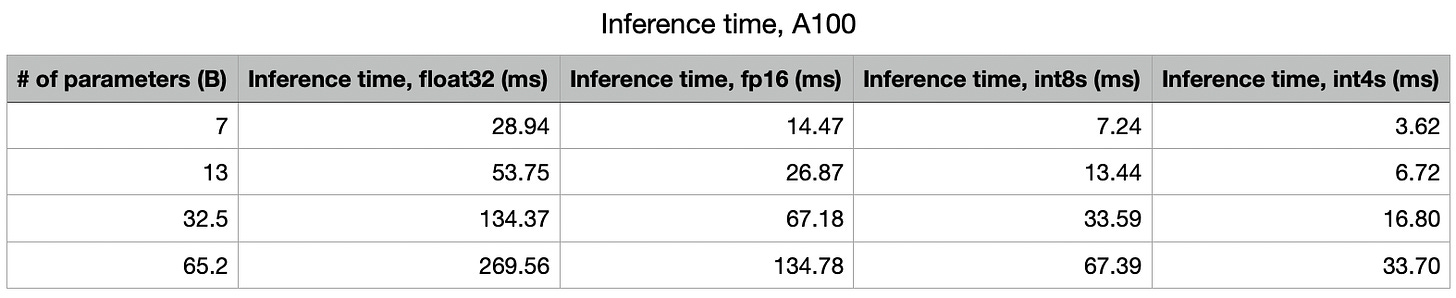
On an A100 (80GB PCIe), the memory bandwidth is 1935GB/s. The int4 compute is 1248 TOPS. As such, the model is (heavily) memory-bound. We should expect to see roughly 30 tokens/s with the 65B model, and 277 tokens/s with the 7B model.
Running LLaMa on a Macbook
The M1 GPU has a bandwidth of 68.25 GB/s, while the M1 GPU can do up to 5.5 TFLOPS of fp16 compute. As such, we should expect a ceiling of ~1 tokens/s for sampling from the 65B model with int4s, and 10 tokens/s with the 7B model.
As the M2 Pro has 200 GB/s of bandwidth, and the M2 Max has 400 GB/s of bandwidth, we should expect massive improvements with them, going up to 6 tokens/s with the M2 Max with the 65B model. That’s pretty darn good for a laptop.
Running LLaMa on a Raspberry Pi 4
A Raspberry Pi 4 has 13.5 GFLOPS of compute, and ~4GB/s of memory bandwidth. Given this, we’d expect to see ~2 tokens/s with the 7B model if it was memory bound. Given that we’re currently seeing ~0.1 tokens/s, I suspect we’re actually compute-bound (although this is a stab in the dark— I can’t find enough information about the specs for a Raspberry Pi to determine this with any precision).
Summary
Memory bandwidth is the limiting factor in almost everything to do with sampling from transformers. Anything that reduces the memory requirements for these models makes them much easier to serve— like quantization! This is yet another reason why distillation, or just training smaller models for longer, is really important.
Note: I’m not an expert in CUDA, so I probably have errors in my math. If so, please let me know— I’ll update the post and credit you.
Resources on transformer inference performance:
Thank you to Kaushik Patnaik, immortal_333, and Arthur Allshire for reading & commenting on early drafts of this, and Salim Fakhohuri + Shuming Hu for pointing out errors in my math.
Errors that have been corrected from earlier versions:
I was missing the batch term in the latency_compute equation.
I had an extra factor of 2 in the latency_memory equation.
I learned almost all of the math surrounding transformer performance from their article; they deserve full credit.
Although we obviously don’t need to calculate the number of parameters for the LLaMa models, as we know them. The equation is useful as a sanity check.
For a more detailed discussion showing that this is the case, check out kipply’s article.
I hedge with “almost” here, but I’m not aware of any counterexamples.



Wow, this was super helpful - probably the most intuitive write up on LLM hardware economics that I’ve read anywhere.
One question for you - how does the length of the context window fit into this equation? AFAIK, longer context windows are more computationally expensive, even if you don’t fill them with tokens. How do you account for that in your calculations?
I tried to work out the math when you describe the optimal batch size for memory bound vs compute bound and I think there may be an error. The multiplicative factor of B (batch size) should be with the compute latency calculation.
Kipply's blog also has the same - https://kipp.ly/transformer-inference-arithmetic/#batch-sizes